引言
支持向量机(Support Vector Machine, SVM)是一种经典的二分类模型,它的核心思想是:在特征空间中寻找一个决策边界(超平面),使得两类样本被正确分开,并且离决策边界最近的样本点(即支持向量)到该边界的距离尽可能大。这个距离被称为间隔(Margin),SVM因此也被称为最大间隔分类器。
决策函数
$$ \left\{ (x_1^{(1)}, x_2^{(1)}, \ldots, x_n^{(1)}), (x_1^{(2)}, x_2^{(2)}, \ldots, x_n^{(2)}), \ldots, (x_1^{(m)}, x_2^{(m)}, \ldots, x_n^{(m)}) \right\} $$
这是一个样本集,包含 $ m $ 个样本,每个样本有 $ n $ 个特征。
- 第 $ i $ 个样本为:$(x_1^{(i)}, x_2^{(i)}, \ldots, x_n^{(i)})$
- 上标 $(i)$ 表示第 $ i $ 个样本
- 下标 $ j $ 表示该样本的第 $ j $ 个特征
- 所以 $ x_j^{(i)} $ 表示 第 $ i $ 个样本的第 $ j $ 个特征值
矩阵表示法(每一行是一个样本,每一列是一个特征):
$$
\mathbf{X} =
\begin{bmatrix}
x_1^{(1)} & x_2^{(1)} & \cdots & x_n^{(1)} \\
x_1^{(2)} & x_2^{(2)} & \cdots & x_n^{(2)} \\
\vdots & \vdots & \ddots & \vdots \\
x_1^{(m)} & x_2^{(m)} & \cdots & x_n^{(m)}
\end{bmatrix}
$$
SVM的决策函数为线性函数:
$$ f(\mathbf{x}) = \mathbf{w}^\top \mathbf{x} + b $$
其中 $\mathbf{w} \in \mathbb{R}^n$ 是权重向量(法向量),$b \in \mathbb{R}$ 是偏置项。决策边界(超平面)由方程 $\mathbf{w}^\top \mathbf{x} + b = 0$ 定义。
对于二维情况,决策边界是一条直线;对于三维情况,它是一个平面;更高维则称为超平面,如:
当样本有两个特征时(即2维),决策边界为直线:
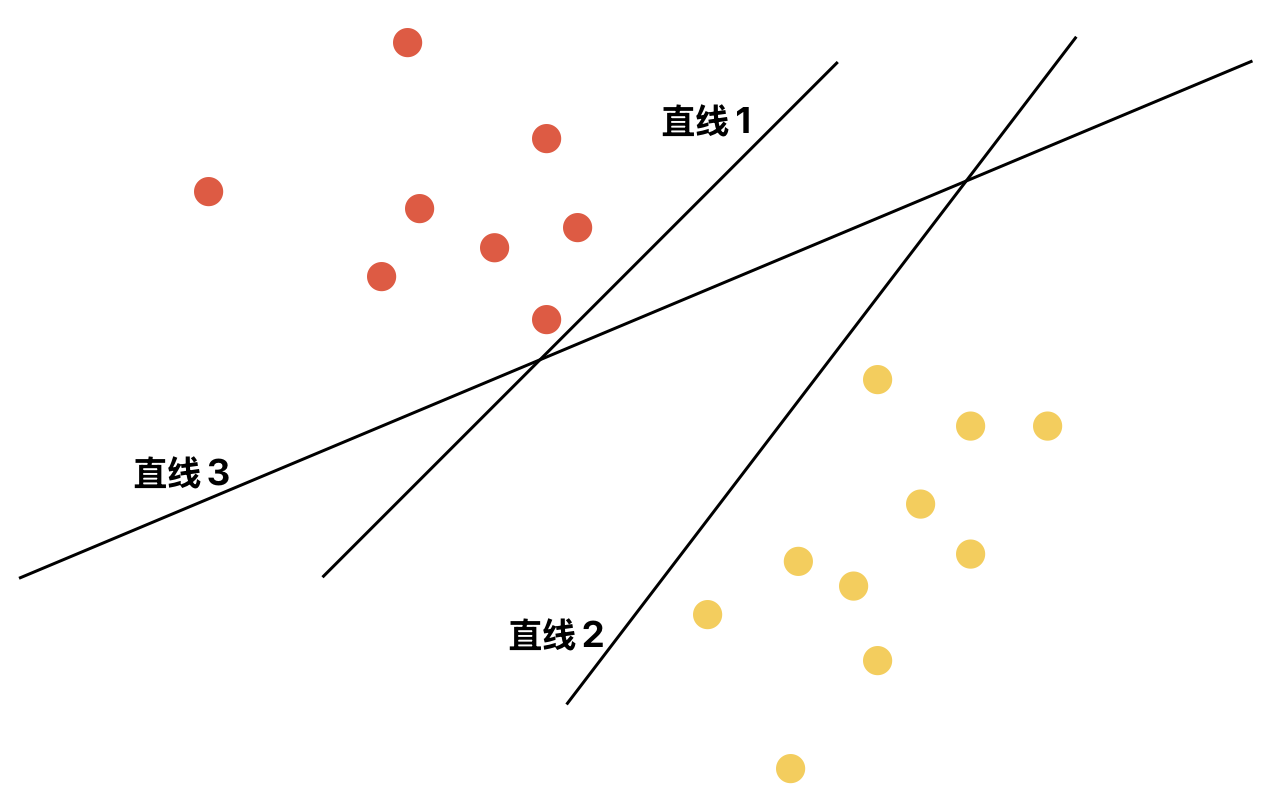 $$
w_1x_1 + w_2x_2 + b = 0
$$
$$
w_1x_1 + w_2x_2 + b = 0
$$
当三个(或多个)特征时,决策边界为平面:
$$
w_1x_1 + w_2x_2 + w_3x_3 + b = 0
$$
分类规则:把 $x^{(i)}$ 代入决策方程:
得到的值$\mathbf{w}^\top \mathbf{x} + b > 0$: $y^{(i)}$ 为正例,$y^{(i)} = +1$;
得到的值$\mathbf{w}^\top \mathbf{x} + b < 0$ : $y^{(i)}$ 为负例,$y^{(i)} = -1$;
因此,正确分类的样本满足 $y^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b) > 0$。
间隔(Margin)与优化目标
距离计算
点到直线的距离
在二维空间中,假设有一条直线的方程为 $ ax + by + c = 0 $,以及一个点 $P(x_0, y_0) $。该点到直线的距离 $d $ 可以通过以下公式计算:
$$
d = \frac{|ax_0 + by_0 + c|}{\sqrt{a^2 + b^2}}
$$
这里,$a, b, c $ 是直线方程的系数,而 $x_0, y_0 $ 是点的坐标。
点到平面的距离
在三维空间中,假设有一个平面的方程为 $Ax + By + Cz + D = 0 $,以及一个点 $P(x_0, y_0, z_0) $。该点到平面的距离 $d $ 可以通过以下公式计算:
$$
d = \frac{|Ax_0 + By_0 + Cz_0 + D|}{\sqrt{A^2 + B^2 + C^2}}
$$
这里,$A, B, C, D $ 是平面方程的系数,而 $x_0, y_0, z_0 $ 是点的坐标。
注:
- 在这两个公式中,分子部分表示的是点代入直线或平面方程后的值的绝对值,它反映了点相对于直线或平面的位置。
- 分母部分是对直线或平面法向量长度的计算(即向量 $(a, b) $ 或 $(A, B, C) $ 的模长),用于标准化距离。
函数间隔
函数间隔(Functional Margin)的定义
对于一个样本 $(\mathbf{x}^{(i)}, y^{(i)})$,其中 $y^{(i)} \in \{+1, -1\}$,我们定义其函数间隔为:
$$ \hat{\gamma}_i = y^{(i)} (\mathbf{w}^\top \mathbf{x}^{(i)} + b) $$
- $\mathbf{w}^\top \mathbf{x}^{(i)} + b$ 是模型对样本 $\mathbf{x}^{(i)}$ 的原始打分(score)。
- 如果分类正确$ y^{(i)}$ 与 $ \mathbf{w}^\top \mathbf{x}^{(i)} + b$ 同号,它的绝对值越大,说明分类的置信度越高。
几何间隔(优化目标)
我们以二维决策边界为例:
$$
w_1x_1 + w_2x_2 + b = 0,其中 \mathbf{w}=[w_1,w_2]
$$
点到决策边界直线的距离为:
$$
\gamma_i = d_i= \frac{|w_1x_1^{(i)} + w_2x_1^{(i)} + b|}{\sqrt{w_1^2 + w_2^2}} = y^{(i)} \frac{w_1x_1^{(i)} + w_2x_1^{(i)} + b}{\sqrt{w_1^2 + w_2^2}} = y^{(i)} \frac{\mathbf{wx} + b}{\sqrt{w_1^2 + w_2^2}} = = y^{(i)} \frac{\mathbf{wx} + b}{\|\mathbf{w}\|}
$$
$\|\mathbf{w}\|$ 为L2范数(也称为欧几里得范数)定义为: $\|\mathbf{w}\| = \sqrt{w_1^2 + w_2^2}$ , 表示的是权重向量 $ \mathbf{w} $ 的长度。
所以几何间隔为:
$$
\gamma_i = y^{(i)} \frac{\mathbf{wx} + b}{\|\mathbf{w}\|} = \frac{1}{\|\mathbf{w}\|} y^{(i)}{(\mathbf{wx} + b)} = \frac{1}{\|\mathbf{w}\|} \hat{\gamma}_i
$$
我们的优化目标是最大化距离决策边界最小的样本的间隔值。
函数间隔VS几何间隔
$$ \gamma_i = \frac{\hat{\gamma}_i}{\|\mathbf{w}\|} $$
| 特性 | 函数间隔 $\hat{\gamma}_i$ | 几何间隔 $\gamma_i$ |
|---|---|---|
| 是否依赖 $\mathbf{w}$ 的尺度 | 是(可任意缩放) | 否(尺度不变) |
| 是否表示真实距离 | 否 | 是 |
| 优化目标 | 不直接用于最大化(因可缩放) | 用于 SVM 的核心目标:最大化最小几何间隔 |
示例:
假设 $\mathbf{w} = (2, 2), b = -2$,对某个样本 $\mathbf{x} = (1,1), y=+1$:
- 函数间隔:$\hat{\gamma} = 1 \cdot (2*1 + 2*1 - 2) = 2$
- 几何间隔:$\gamma = 2 / \sqrt{2^2 + 2^2} = 2 / \sqrt{8} = \frac{1}{\sqrt{2}}$
现在把 $\mathbf{w}, b$ 都乘以 10:
- $\mathbf{w}' = (20,20), b' = -20$
- 函数间隔变为:$20$(变大了!)
- 但几何间隔仍是:$20 / \sqrt{800} = 20 / (10\sqrt{8}) = 2 / \sqrt{8} = \frac{1}{\sqrt{2}}$
几何间隔不变,函数间隔随参数缩放而变。
最大间隔思想
SVM的目标是:找到一个超平面 $(\mathbf{w},b)$,使得所有样本中离它最近的那个样本的几何间隔尽可能大。这个最近的样本点就是支持向量(Support Vector)。
整个数据集的几何间隔定义为:
$$ \gamma = \min_{i=1,\dots,m} \gamma_i $$
优化问题即为:
$$ \max_{\mathbf{w},b} \gamma = \max_{\mathbf{w},b} \min_{i} \frac{y^{(i)}(\mathbf{w}^\top \mathbf{x}^{(i)} + b)}{\|\mathbf{w}\|} $$
目标函数与化简
SVM 的核心思想是:找到一个决策边界,使得所有样本中离它最近的那个样本(即支持向量)的距离尽可能大。
单个样本的几何间隔:
$$ \gamma_i = \frac{1}{\|\mathbf{w}\|} y^{(i)}(\mathbf{w}^\top \mathbf{x}_i + b) $$整个数据集的几何间隔是所有样本中最小的那个:
$$ \gamma = \min_{i=1,\dots,m} \gamma_i $$我们的目标是找到能最大化这个最小几何间隔的参数:
$$ \max_{\mathbf{w}, b} \gamma = \max_{\mathbf{w}, b} \min_{i=1,\dots,m} \frac{1}{\|\mathbf{w}\|} y^{(i)}(\mathbf{w}^\top \mathbf{x}_i + b) $$对间隔进行缩放:
性质:对同一超平面,对参数($\mathbf{w}$ 和 $b$ )同时进行缩放,几何间隔保持不变,函数间隔发生变化。
$$ \gamma_i = \frac{1}{\|\mathbf{w}\|} y^{(i)}(\mathbf{w}^\top \mathbf{x}_i + b) $$
设对任意正实数 $c>0$,把参数变为 $(\mathbf w',b')=(c\mathbf w,c b)$。
超平面方程由 $\mathbf w^\top \mathbf x + b =0$ 变为 $(c\mathbf w)^\top \mathbf x + c b = c(\mathbf w^\top \mathbf x + b)$。零点集不变,因此超平面本身不变(同一条直线/平面)。
函数边距变为
$$ \hat\gamma_i' = y_i((c\mathbf w)^\top \mathbf x_i + c b) = c, y_i(\mathbf w^\top \mathbf x_i + b) = c,\hat\gamma_i. $$
所以函数边距按同样因子 (c) 缩放。$\mathbf w 的范数变成 |\mathbf w'|=|c\mathbf w| = c|\mathbf w|$。
几何边距变为
$$ \gamma_i' = \frac{\hat\gamma_i'}{|\mathbf w'|} = \frac{c\hat\gamma_i}{c|\mathbf w|} = \frac{\hat\gamma_i}{|\mathbf w|} = \gamma_i. $$也就是说,几何边距不变,函数间隔变为原来的c倍。
我们对 $\max_{\mathbf{w}, b} \gamma = \max_{\mathbf{w}, b} \min_{i=1,\dots,m} \frac{1}{\|\mathbf{w}\|} y^{(i)}(\mathbf{w}^\top \mathbf{x}_i + b)$ 中的$\frac{1}{\|\mathbf{w}\|} y^{(i)}(\mathbf{w}^\top \mathbf{x}_i + b)$ 进行缩放(不会改变原来的结果值),缩放到 $y^{(i)}(\mathbf{w}^\top \mathbf{x}_i + b) \ge 1$,此时:
$$ \begin{aligned} &\max_{\mathbf{w}, b} \gamma = \max_{\mathbf{w}, b} \min_{i=1,\dots,m} \frac{1}{\|\mathbf{w}\|} y^{(i)}(\mathbf{w}^\top \mathbf{x}_i + b) = \max_{\mathbf{w}, b} \min_{i=1,\dots,m} \frac{1}{\|\mathbf{w}\|} \cdot 1 = \max_{\mathbf{w}, b}\frac{1}{\|\mathbf{w}\|} = \min_{\mathbf{w}, b}{\|\mathbf{w}\|} = \min_{\mathbf{w}, b}\frac{1}{2}{\|\mathbf{w}\|}^2 \\ &\text{s.t.}\quad y_i(\mathbf w^\top \mathbf x_i + b) \ge 1,\quad i=1,\dots,m. \end{aligned} $$
所以,SVM优化目标的的原始形式为:
$$ \begin{aligned} &\min_{\mathbf{w}, b}\frac{1}{2}{\|\mathbf{w}\|}^2 \\ &\text{s.t.}\quad y_i(\mathbf w^\top \mathbf x_i + b) \ge 1,\quad i=1,\dots,m. \end{aligned} $$
加入软间隔,在目标里加上松弛项并引入松弛变量 $\xi_i$ 的优化目标形式为:
$$ \begin{aligned} &\min \tfrac{1}{2}|\mathbf w|^2 + C\sum_{i=1}^n\xi_i \\ &\text{s.t.}\quad y_i(\mathbf w^\top \mathbf x_i + b) \ge 1-\xi_i,\ \xi_i\ge 0, \quad i=1,\dots,m. \end{aligned} $$
硬间隔与软间隔
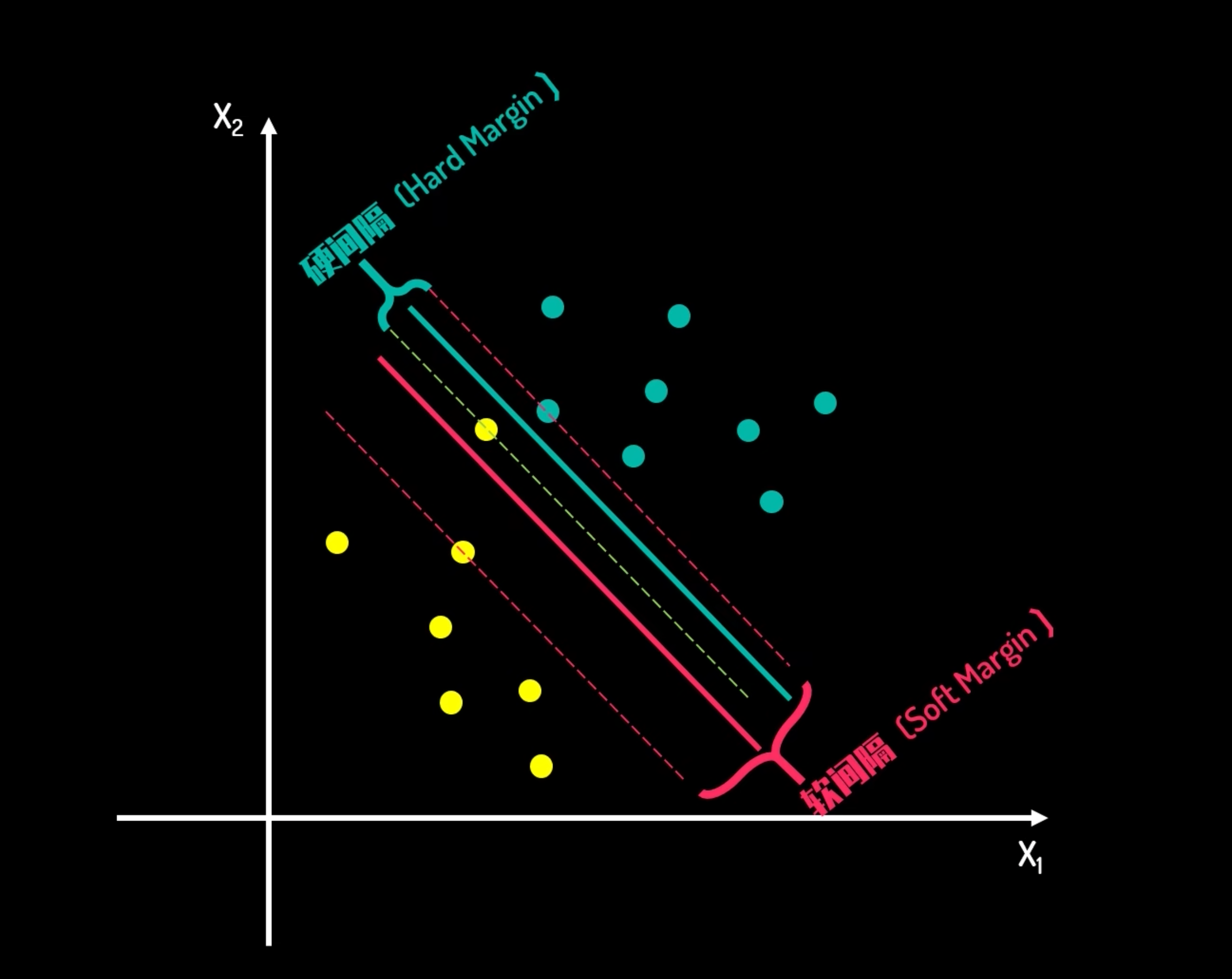
硬间隔
- 前提:数据完全线性可分。
- 目标:找到一个超平面,使得所有样本被正确分类,且间隔最大。
- 数学形式:
$$ \begin{aligned} &\min_{\mathbf{w}, b} \frac{1}{2} \|\mathbf{w}\|^2 \\ &\text{s.t. } y_i(\mathbf{w}^\top \mathbf{x}_i + b) \geq 1,\quad i=1,\dots,m \end{aligned} $$
其中 $y_i \in \{-1, +1\}$
软间隔
现实情况:数据可能含噪声或轻微不可分。
引入松弛变量 $\xi_i \geq 0$,允许部分样本违反约束。
目标函数加入正则项(控制间隔与误分类的权衡):
$$ \begin{aligned} &\min_{\mathbf{w}, b, \xi} \frac{1}{2} \|\mathbf{w}\|^2 + C \sum_{i=1}^m \xi_i \\ &\text{s.t. } y_i(\mathbf{w}^\top \mathbf{x}_i + b) \geq 1 - \xi_i,\quad \xi_i \geq 0 \end{aligned} $$- $C$ 是惩罚系数:$C$ 越大,对误分类越敏感(趋向硬间隔);$C$ 小则容忍更多误分类。
- 如果 $ ξ_i = 0 $,点被正确分类且在间隔之外。
- 如果 $ 0 < ξ_i <= 1 $,点被正确分类但在间隔之内。
- 如果 $ ξ_i > 1 $,点被错误分类。
拉格朗日对偶求解(硬间隔)
拉格朗日函数
上述我们已经得到SVM的优化目标函数为:
$$
\begin{aligned}
&\min_{\mathbf{w}, b} \frac{1}{2} \|\mathbf{w}\|^2 \\
&\text{s.t. } y_i(\mathbf{w}^\top \mathbf{x}_i + b) - 1 \geq 0,\quad i=1,\dots,m
\end{aligned}
$$
目标函数是一个带不等式约束的凸二次规划(QP)问题。我们可以用拉格朗日乘子法将其转化为一个更易于求解的对偶问题。
步骤 1: 引入拉格朗日函数
为每个不等式约束引入一个拉格朗日乘子 $\alpha_i \ge 0$,构建拉格朗日函数:
$$
\mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha}) = \frac{1}{2} \|\mathbf{w}\|^2 - \sum_{i=1}^m \alpha_i \left[ y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 \right]
$$
- $\boldsymbol{\alpha} = (\alpha_1, \dots, \alpha_m)^T$
- 从上述式子不难看出:$\mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha}) \leq \frac{1}{2} \|\mathbf{w}\|^2$
根据拉格朗日乘子法的性质,原始问题等价于以下无约束的极小极大问题,所以目标函数转换为:
$$
\min_{\mathbf{w}, b} \max_{\boldsymbol{\alpha} \ge 0} \mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha})
$$
步骤 2: 转化为对偶问题(Dual Problem)
原始问题是 $\min_{\mathbf{w}, b} \max_{\boldsymbol{\alpha} \ge 0} \mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha})$。在满足KKT条件的情况下,我们可以等价地求解它的对偶问题:
$$
\min_{\mathbf{w}, b} \max_{\boldsymbol{\alpha} \ge 0} \mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha})
\ → \
\max_{\boldsymbol{\alpha} \ge 0} \min_{\mathbf{w}, b} \mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha})
$$
首先,求解内层的最小化问题: $\min_{\mathbf{w}, b} \mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha})$
分别对 $\mathbf{w}$ 和 $b$ 求偏导并令其为零:
$$
\nabla_{\mathbf{w}} \mathcal{L} = \mathbf{w} - \sum_{i=1}^m \alpha_i y_i \mathbf{x}_i = 0 \quad \Rightarrow \quad \mathbf{w} = \sum_{i=1}^m \alpha_i y_i \mathbf{x}_i
$$
$$ \nabla_{\mathbf{b}} \mathcal{L} = \frac{\partial \mathcal{L}}{\partial b} = - \sum_{i=1}^m \alpha_i y_i = 0 \quad \Rightarrow \quad \sum_{i=1}^m \alpha_i y_i = 0 $$
将这两个结果代回拉格朗日函数 $\mathcal{L}$:
$$
\begin{aligned}
\mathcal{L}(\mathbf{w}, b, \boldsymbol{\alpha}) &= \frac{1}{2} \left( \sum_{i=1}^m \alpha_i y_i \mathbf{x}_i \right)^T \left( \sum_{j=1}^m \alpha_j y_j \mathbf{x}_j \right) - \sum_{i=1}^m \alpha_i y_i \mathbf{x}_i^T \left( \sum_{j=1}^m \alpha_j y_j \mathbf{x}_j \right) - b \sum_{i=1}^m \alpha_i y_i + \sum_{i=1}^m \alpha_i \\
&= \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j - \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j + \sum_{i=1}^m \alpha_i \\
&= -\frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j + \sum_{i=1}^m \alpha_i
\end{aligned}
$$
(注意:中间项 $- b \sum_{i=1}^m \alpha_i y_i$ 因为 $\sum \alpha_i y_i = 0$ 而消失了。)
步骤 3: 得到对偶问题
现在,我们的目标变成了最大化上面这个结果,同时要满足约束:
$$
\begin{aligned}
& \max_{\boldsymbol{\alpha}} \quad -\frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j + \sum_{i=1}^m \alpha_i \\
& \text{s.t.} \quad \sum_{i=1}^m \alpha_i y_i = 0, \\
& \quad \quad \alpha_i \ge 0, \quad i = 1, \dots, m
\end{aligned}
$$
通常我们将最大化转换为最小化,得到SVM标准对偶问题的最终形式:
$$ \begin{aligned} & \min_{\boldsymbol{\alpha}} \quad \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j - \sum_{i=1}^m \alpha_i \\ & \text{s.t.} \quad \sum_{i=1}^m \alpha_i y_i = 0, \\ & \quad \quad \alpha_i \ge 0, \quad i = 1, \dots, m \end{aligned} $$
然后就是根据所有样本的值带入上式(还有约束条件),求得 $\alpha$,再根据 $w$ 与$\alpha$的关系求得 $w$值。
在根据 $y = \mathbf{w}^\top \mathbf{x}_i + b$ 随边找一个样本点带入求得 $b$ 值。
$\alpha$的意义:
所有$\alpha_i$ 不为零的点就是支持向量,也就是位于边界上的点,非边界上的点$\alpha = 0$
KKT条件与支持向量
求解上述对偶问题后,我们得到最优的拉格朗日乘子 $\boldsymbol{\alpha}^*$。此时,KKT条件(最优解必须满足的条件)起着关键作用,特别是其中的互补松弛条件:
$$
\alpha_i^* \left[ y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 \right] = 0, \quad \forall i
$$
这个条件意味着:
- 如果 $\alpha_i^* = 0$,那么对应的样本点不会对 $\mathbf{w}$ 的计算产生影响(见 $\mathbf{w} = \sum \alpha_i y_i \mathbf{x}_i$)。
- 如果 $\alpha_i^* > 0$,那么必然有 $y_i (\mathbf{w}^T \mathbf{x}_i + b) = 1$。这意味着这个样本点正好在最大间隔边界上!
这些 $\alpha_i^* > 0$ 所对应的样本点,就是支持向量(Support Vectors)。它们决定了最终的超平面。
求解 $\mathbf{w}$ 和 $b$:
$\mathbf{w}$: 我们已经从导数为零的条件得到了:
$$ \mathbf{w}^* = \sum_{i=1}^m \alpha_i^* y_i \mathbf{x}_i $$
实际上,我们只需要支持向量(即 $\alpha_i^* > 0$ 的点)来计算:
$$ \mathbf{w}^* = \sum_{i \in SV} \alpha_i^* y_i \mathbf{x}_i $$$b$: 利用任何一个支持向量 $(\mathbf{x}_s, y_s)$(即满足 $\alpha_s^* > 0$ 的点),根据互补松弛条件:
$$ y_s (\mathbf{w}^{*T} \mathbf{x}_s + b^*) = 1 $$
可以解出:
$$ b^* = y_s - \mathbf{w}^{*T} \mathbf{x}_s $$
为了数值稳定性,通常使用所有支持向量计算出的 $b$ 的平均值。
拉格朗日对偶与求解(软间隔)
松弛变量与惩罚参数
优化问题(原始问题,Primal Problem with Soft Margin):
由于数据可能不是线性可分的,我们引入松弛变量(Slack Variables) $\xi_i \ge 0$ 来允许一些样本犯错误。同时,在目标函数中加入对这些错误的惩罚项。优化问题变为:
$$ \begin{aligned} & \min_{\mathbf{w}, b, \boldsymbol{\xi}} \quad \frac{1}{2} \|\mathbf{w}\|^2 + C \sum_{i=1}^m \xi_i \\ & \text{s.t.} \quad y_i (\mathbf{w}^T \mathbf{x}_i + b) \ge 1 - \xi_i, \quad i = 1, \dots, m \\ & \quad \quad \xi_i \ge 0, \quad i = 1, \dots, m \end{aligned} $$
这里:
- $\xi_i$ 是松弛变量。$\xi_i = 0$ 表示样本 $x_i$ 被正确分类且位于间隔边界之外;$0 < \xi_i \le 1$ 表示样本位于间隔内部,但在正确的一侧;$\xi_i > 1$ 表示样本被错误分类。
- $C > 0$ 是惩罚参数,由用户指定。它控制了我们对分类错误的容忍度:
- $C$ 越大,对错误的惩罚越重,间隔带越“硬”,可能过拟合。
- $C$ 越小,对错误的惩罚越轻,间隔带越“宽软”,可能欠拟合。
构建拉格朗日函数:
我们现在有两个不等式约束,因此引入两组拉格朗日乘子:$\alpha_i \ge 0$ 和 $\mu_i \ge 0$。
$$ \mathcal{L}(\mathbf{w}, b, \boldsymbol{\xi}, \boldsymbol{\alpha}, \boldsymbol{\mu}) = \frac{1}{2} \|\mathbf{w}\|^2 + C \sum_{i=1}^m \xi_i - \sum_{i=1}^m \alpha_i \left[ y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i \right] - \sum_{i=1}^m \mu_i \xi_i $$
转化为对偶问题:
同样,我们求解 $\min_{\mathbf{w}, b, \boldsymbol{\xi}} \max_{\boldsymbol{\alpha}, \boldsymbol{\mu} \ge 0} \mathcal{L}$ 的对偶问题 $\max_{\boldsymbol{\alpha}, \boldsymbol{\mu} \ge 0} \min_{\mathbf{w}, b, \boldsymbol{\xi}} \mathcal{L}$。
对 $\mathbf{w}, b, \xi_i$ 求偏导并令为零:
$$ \nabla_{\mathbf{w}} \mathcal{L} = \mathbf{w} - \sum_{i=1}^m \alpha_i y_i \mathbf{x}_i = 0 \quad \Rightarrow \quad \mathbf{w} = \sum_{i=1}^m \alpha_i y_i \mathbf{x}_i $$$$ \frac{\partial \mathcal{L}}{\partial b} = - \sum_{i=1}^m \alpha_i y_i = 0 \quad \Rightarrow \quad \sum_{i=1}^m \alpha_i y_i = 0 $$
$$ \frac{\partial \mathcal{L}}{\partial \xi_i} = C - \alpha_i - \mu_i = 0 \quad \Rightarrow \quad \alpha_i + \mu_i = C $$
将结果代回拉格朗日函数:
将 $\mathbf{w} = \sum \alpha_i y_i \mathbf{x}_i$, $\mu_i = C - \alpha_i$ 代入 $\mathcal{L}$。经过与硬间隔类似的化简过程(注意包含 $\xi_i$ 的项会相互抵消),我们得到:
对偶问题(Dual Problem with Soft Margin):
$$
\boxed{
\begin{aligned}
& \min_{\boldsymbol{\alpha}} \quad \frac{1}{2} \sum_{i=1}^m \sum_{j=1}^m \alpha_i \alpha_j y_i y_j \mathbf{x}_i^T \mathbf{x}_j - \sum_{i=1}^m \alpha_i \\
& \text{s.t.} \quad \sum_{i=1}^m \alpha_i y_i = 0, \\
& \quad \quad 0 \le \alpha_i \le C, \quad i = 1, \dots, m
\end{aligned}
}
$$
关键变化: 与硬间隔相比,软间隔的对偶问题唯一的变化是约束条件从 $\alpha_i \ge 0$ 变成了 $0 \le \alpha_i \le C$。这个上界 $C$ 来自于关系式 $\alpha_i = C - \mu_i$ 和 $\mu_i \ge 0$。
KKT条件与支持向量
对于软间隔SVM,KKT条件(最优解必须满足的条件)变得更加丰富,它们完整地描述了支持向量的不同类型。
KKT条件:
平稳性: $\mathbf{w} = \sum_{i=1}^m \alpha_i y_i \mathbf{x}_i$, $\sum_{i=1}^m \alpha_i y_i = 0$, $\alpha_i + \mu_i = C$.
原始可行性: $y_i (\mathbf{w}^T \mathbf{x}_i + b) \ge 1 - \xi_i$, $\xi_i \ge 0$.
对偶可行性: $\alpha_i \ge 0$, $\mu_i \ge 0$.
互补松弛性:
$$ \alpha_i \left[ y_i (\mathbf{w}^T \mathbf{x}_i + b) - 1 + \xi_i \right] = 0 $$$$ \mu_i \xi_i = 0 $$
根据这些KKT条件,我们可以将样本点分为三类:
| $\alpha_i$ 的值 | $\xi_i$ 的值 | 几何位置 | 类型 |
|---|---|---|---|
| $\alpha_i = 0$ | $\xi_i = 0$ | 被正确分类,在间隔边界之外 | 非支持向量 |
| $0 < \alpha_i < C$ | $\xi_i = 0$ | 恰好落在间隔边界上 ($y_i(\mathbf{w}^T\mathbf{x}_i + b) = 1$) | 标准支持向量 |
| $\alpha_i = C$ | $0 < \xi_i \le 1$ | 位于间隔内部,但在正确的一侧 | 边界支持向量 |
| $\alpha_i = C$ | $\xi_i > 1$ | 在错误的一侧,被误分类 | 误分类支持向量 |
求解 $\mathbf{w}$ 和 $b$:
$\mathbf{w}^*$ 的求解与硬间隔相同,只依赖于支持向量 ($\alpha_i > 0$):
$$ \mathbf{w}^* = \sum_{i=1}^m \alpha_i^* y_i \mathbf{x}_i = \sum_{i \in SV} \alpha_i^* y_i \mathbf{x}_i $$$b^*$ 的求解:在硬间隔中,我们使用任意一个支持向量。在软间隔中,为了数值稳定性,我们通常使用所有标准支持向量 ($0 < \alpha_i < C$) 来计算 $b$ 的平均值。
对于任何一个标准支持向量,由于 $\xi_i = 0$ 且 $0 < \alpha_i < C$,根据互补松弛条件有:
$$ y_i (\mathbf{w}^{*T} \mathbf{x}_i + b^*) = 1 $$
因此,
$$ b^* = \frac{1}{|S|} \sum_{i \in S} (y_i - \mathbf{w}^{*T} \mathbf{x}_i) $$
其中 $S = \{ i | 0 < \alpha_i < C \}$ 是所有标准支持向量的集合。
最终的决策函数(软间隔版本)
软间隔SVM的最终决策函数在形式上与硬间隔完全相同:
$$ f(\mathbf{x}) = \text{sign}(\mathbf{w}^{*T} \mathbf{x} + b^*) $$
将 $\mathbf{w}^* = \sum_{i \in SV} \alpha_i^* y_i \mathbf{x}_i$ 代入:
$$ \boxed{ f(\mathbf{x}) = \text{sign}\left( \sum_{i \in SV} \alpha_i^* y_i \mathbf{x}_i^T \mathbf{x} + b^* \right) } $$
关键点:
- 形式不变:决策函数仍然是支持向量的线性组合。
- 支持向量更多样:支持向量集合 $SV$ 现在包含了所有 $\alpha_i > 0$ 的样本,即标准支持向量和那些被允许“犯错”的边界/误分类支持向量。正是这些“犯错”的样本使得模型获得了鲁棒性。
- 核函数应用:同样,我们可以将内积 $\mathbf{x}_i^T \mathbf{x}$ 替换为核函数 $K(\mathbf{x}_i, \mathbf{x})$,从而将软间隔SVM应用于非线性分类问题,这被称为非线性软间隔SVM。
软间隔 vs.硬间隔
| 特性 | 硬间隔SVM | 软间隔SVM |
|---|---|---|
| 适用场景 | 数据严格线性可分 | 数据近似线性可分或存在噪声 |
| 优化目标 | $\min \frac{1}{2}\|\mathbf{w}\|^2$ | $\min \frac{1}{2}\|\mathbf{w}\|^2 + C \sum \xi_i$ |
| 对偶约束 | $0 \le \alpha_i$ | $0 \le \alpha_i \le C$ |
| 支持向量 | 都在间隔边界上 | 在间隔边界上、内部或误分点 |
| 参数 | 无 | 惩罚参数 $C$ |
核函数(Kernel Function)
低维不可分与高维映射
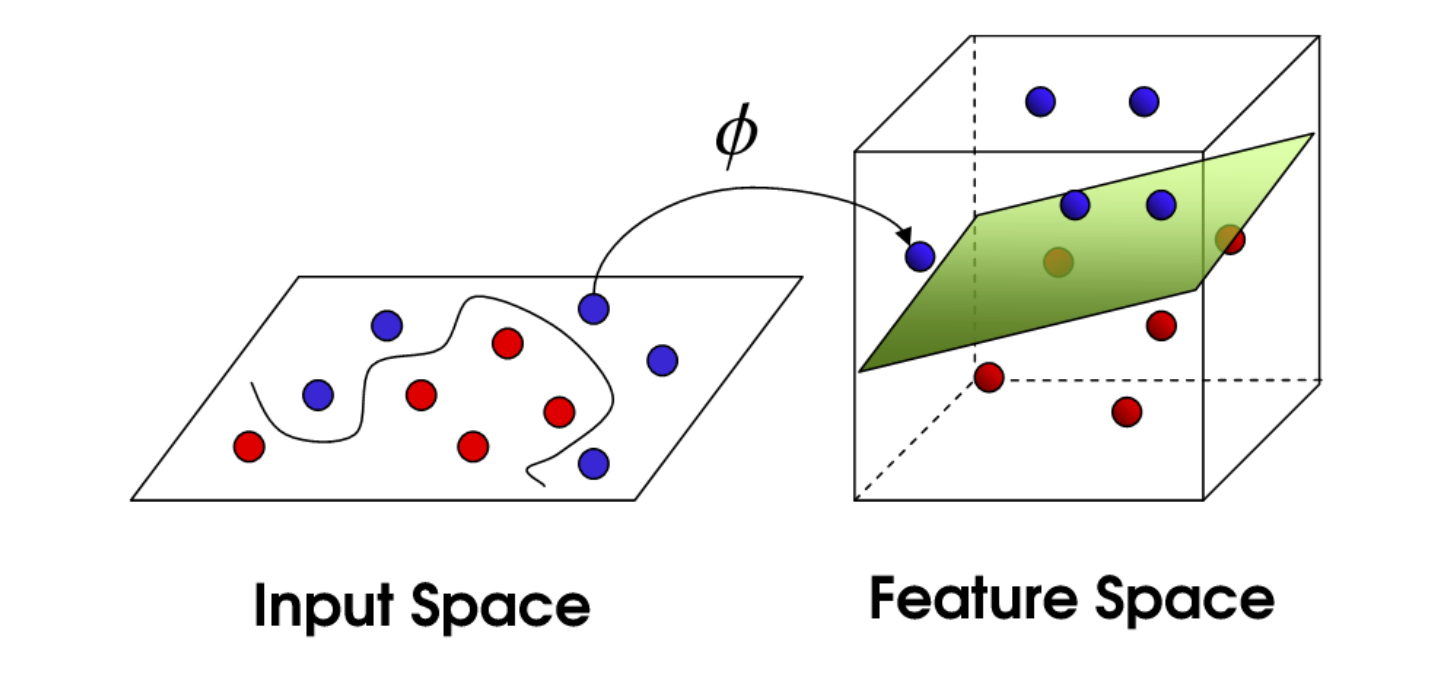
当数据在原始特征空间中线性不可分时,一个自然的想法是将数据映射到更高维的空间,使其变得线性可分。设映射函数为 $\phi(\mathbf{x})$,则在高维空间中的决策函数为:
$$
f(\mathbf{x}) = \mathbf{w}^\top \phi(\mathbf{x}) + b
$$
核技巧(Kernel Trick)
直接计算 $\phi(\mathbf{x})$ 可能非常复杂,甚至无限维。但注意到在对偶问题中,所有涉及样本的地方都是以内积形式出现:$(\mathbf{x}^{(i)})^\top \mathbf{x}^{(j)}$。如果存在一个函数 $K(\cdot,\cdot)$,使得:
$$ K(\mathbf{x}^{(i)}, \mathbf{x}^{(j)}) = \phi(\mathbf{x}^{(i)})^\top \phi(\mathbf{x}^{(j)}) $$
那么我们就可以在低维空间中计算核函数 $K$,而无需显式地计算高维映射 $\phi$,从而大大降低计算量。这就是核技巧。
常用核函数
- 线性核:$K(\mathbf{x}_i, \mathbf{x}_j) = \mathbf{x}_i^\top \mathbf{x}_j$(即无映射,用于线性可分情况)
- 多项式核:$K(\mathbf{x}_i, \mathbf{x}_j) = (\gamma \mathbf{x}_i^\top \mathbf{x}_j + r)^d$
- 高斯核(RBF核):$K(\mathbf{x}_i, \mathbf{x}_j) = \exp(-\gamma \|\mathbf{x}_i - \mathbf{x}_j\|^2)$(最常用,可将特征映射到无穷维)
- Sigmoid核:$K(\mathbf{x}_i, \mathbf{x}_j) = \tanh(\gamma \mathbf{x}_i^\top \mathbf{x}_j + r)$
核函数的选择通常依赖领域知识或交叉验证。
核函数的选取原则
- 若特征数 $n$ 很大,而样本数 $m$ 较小,通常使用线性核(避免过拟合);
- 若 $n$ 适中,$m$ 也适中,可尝试高斯核;
- 若 $n$ 很小,$m$ 很大,需要先手工增加特征,再考虑线性核。
硬间隔、软间隔、核函数对比
| 特性 | 硬间隔SVM | 软间隔SVM | 核SVM |
|---|---|---|---|
| 适用场景 | 数据严格线性可分 | 数据近似线性可分或含噪声 | 非线性可分数据 |
| 优化目标 | $\min \frac12\|\mathbf{w}\|^2$ | $\min \frac12\|\mathbf{w}\|^2 + C\sum\xi_i$ | 在核空间中间接优化 |
| 对偶约束 | $\alpha_i \ge 0$ | $0 \le \alpha_i \le C$ | 同上,但内积换为核函数 |
| 支持向量 | 仅在间隔边界上 | 包括边界、内部、误分类点 | 核空间中的支持向量 |
| 关键参数 | 无 | 惩罚参数 $C$ | 核参数(如 $\gamma$)及 $C$ |
SVM通过最大化间隔获得良好的泛化能力,引入软间隔和核函数后能处理各种复杂数据,是机器学习中非常经典的算法。理解其背后的对偶推导和KKT条件,有助于深入掌握支持向量机的精髓。


